| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- web-proxy lab
- ip
- Error Code: 1055
- strcpy
- SQL
- mysql
- 정글#정글사관학교#3기#내일#기대#설렘#희망#노력
- BSD소켓
- HTTP
- C언어
- DNS
- TCP
- https://coding-factory.tistory.com/641
- group by
- strcat
- https://firecatlibrary.tistory.com/49?category=874970
- Today
- Total
매일을 설렘으로
[Algorithm] 깊이 우선 탐색(DFS)와 너비 우선 탐색(BFS) + 예제 본문
그래프로 탐색하는 방법에는 두 가지가 있다. DFS, BFS.
1) 깊이 우선 탐색 (DFS)
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에
해당 분기를 완벽하게 탐색하는 방식을 말한다.
- 구현 : 스택 또는 재귀함수로 구현 -> 둘 중에 어떤 구조로 짜는지에 대한 장단점은 무엇일까?
2) 너비 우선 탐색 (BFS)
루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법으로,
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법입니다.
- 구현 : 큐를 이용해서 구현
3) 활용 문제 유형 및 응용
- 그래프의 모든 정점을 방문하는 것이 중요한 문제
=> DFS, BFS 둘 다 동일 (∵모든 경로 탐색시 시간 복잡도는 동일)
- 경로의 특징을 저장해둬야하는 문제
: 예를 들면 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용합니다. (BFS는 경로의 특징을 가지지 못합니다)
- 최단거리 구해야 하는 문제
미로 찾기 등 최단거리를 구해야 할 경우, BFS가 유리합니다.
왜냐하면 깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만,
너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리기 때문입니다.
이밖에도
- 검색 대상 그래프가 정말 크다면 DFS를 고려
- 검색대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS
4) 코드 (Python)
- DFS (stack)
- DFS (재귀함수)
- [A/I] stack과 재귀함수 사용간 장단점 차이?
※ 방문이력(흔히 visit 표기)을 확인하는 활용이 다양하다.
- 노드가 양의 정수 (1~N)이라면 리스트의 인덱스와 노드 번호와 연결하여 True/False 줄 수 있다. (∵시간 복잡도 O(1))
- 노드가 일반 텍스트나 인덱스와 매칭이 어렵다면, visit을 딕셔너리의 key로 연결하는 방법도 있다. (∵시간 복잡도 O(1))
- 노드를 append로 하여, not in 연산자를 사용하는 경우 O(N)으로 느려 잘 사용하지 않는다.
def dfs(graph, start_node):
visit = list()
stack = list()
stack.append(start_node)
while stack:
node = stack.pop()
if node not in visit: # 시간 복잡도가 O(N)으로 list_index나 dict로 O(1) 개선가능
visit.append(node)
stack.extend(graph[node]) # graph[node] - visit 원소 빼주면 시간 줄어듬
return visitgraph = list(list())
visited = list()
def dfs(graph, start): # 현재 노드를 방문처리
visited[start] = True
for i in graph[start]: # 현재 노드와 연결된 다른 노드를 재귀적으로 방문
if not visited[i]:
dfs(graph,i) #/재귀함수/#
- BFS (queue) -> from collections import deque
def bfs(graph, start_node):
visit = list()
queue = list()
queue.append(start_node)
while queue:
node = queue.pop(0) # 시간 복잡도 O(N)으로 collections.deque() 함수로 하면 개선 가능
if node not in visit: # 시간 복잡도가 O(N)으로 list_index나 dict로 O(1) 개선가능
visit.append(node)
stack.extend(graph[node]) # graph[node] - visit 원소 빼주면 시간 줄어듬
return visit
참고 자료) dict vs list 값 조회
: dict는 hash table을 사용해서 O(1)가지고, list는 O(N)으로 느리다.
https://stackoverflow.com/questions/38927794/python-dictionary-vs-list-which-is-faster
Python dictionary vs list, which is faster?
I was coding a Euler problem, and I ran into question that sparked my curiosity. I have two snippets of code. One is with lists the other uses dictionaries. using lists: n=100000 num=[] suma=0 f...
stackoverflow.com
참고
https://itholic.github.io/python-bfs-dfs/
[python] 파이썬으로 bfs, dfs 구현해보기
BFS, DFS
itholic.github.io
연습문제 1) 트리의 부모 찾기
- 문제 설명
> 루트 없는 트리가 주어진다. 루트가 1 이라고 가정할 때, 각 노드의 부모를 구해라.
=> 사이클이 없는 그래프이다. 루트가 정해지면 방향성을 갖는 그래프를 구할 수 있다.
> 2번 노드부터 부모 노드 번호를 출력해라.
=> 모든 노드를 탐색해야하므로, DFS나 BFS 방식을 모두 사용가능할 것 같다.
-> [A/I] 실제 그런지 BFS 구현해보자
- 코드 설명
> DFS 재귀함수 이용
-> [A/I] stack방식과 재귀방식 중 장단점 확인
> Parents 리스트를 visit 리스트 대신에 사용함.
import sys
import collections
sys.setrecursionlimit(1000000000)
n = int(sys.stdin.readline())
graph = collections.defaultdict(list) # dict의 value타입을 기본적으로 list로 선언
for _ in range(n-1):
s, e = map(int, sys.stdin.readline().split())
graph[s].append(e)
graph[e].append(s)
#parents = [0, 1, 2, 3, 4, 5]
parents = [0 for i in range(n+1)]
def DFS(graph, node):
# root들이 연결하고 있는 자식 노드를 확인하고, 저장하고 각각의 자식노드를 또 확인하고 저장하고 재귀..
for child in graph[node]:
if parents[child] == 0: # visit를 대신 parent 값이 갱신됐는지 확인
parents[child] = node # parent 값 갱신한다. (방문 체크)
DFS(graph, child) # 재귀함수 이용
DFS(graph, 1)
for i in range(2, n+1):
print(parents[i])연습문제 2) 구슬 찾기
- 문제 설명
> 무게가 다른 N개의 구슬 (1,2,3,,,,N). 무게가 중간인 원소가 될 수 없는 원소의 갯수를 구하라
> 구슬간 무게가 비교 결과가 M개 존재한다.
-> 비교된 구슬간 간선이 존재하고 방향성 또한 존재한다.
-> 손자 노드들의 갯수가 과반 이상이라면, 해당 노드는 제외 대상이다.
> 큰 쪽/ 작은 쪽을 모두 제외해야되기 때문에 graph는 큰 쪽 방향으로의 그래프, 작은 쪽 방향으로의 그래프가 필요.
- 코드 설명
> 문제의 조건에 손자 노드의 갯수가 과반이상이라면, 제외 대상이므로 모든 노드를 볼 필요가 없고, 손자 노드를 카운팅해나가면서 커트를 해줄 수 있다. (DFS 적합)
> 제외 대상 갯수가 구하는 목적이기 때문에 탐색하고 중간 무게 후보로 가능한지, 못한지 체크해서 return 1/0
- Action Item
> 루트가 명확하지 않아 모든 노드를 DFS로 확인했는데, 줄일 수 있는 방법이 있을까? (DP?)
import sys
n, m = map(int, sys.stdin.readline().split())
graph_b = [[]*(n+1) for _ in range(n+1)]
graph_s = [[]*(n+1) for _ in range(n+1)]
mid = n//2
for i in range(m):
b, s = map(int, sys.stdin.readline().split())
graph_b[s].append(b)
graph_s[b].append(s)
def DFS(start, graph):
visited = [False] * (n+1)
stack = [start]
visited[start] = True
cnt = 0
while stack:
num = stack.pop()
for i in graph[num]:
if not visited[i]:
visited[i] = True
stack.append(i)
cnt += 1
if cnt > mid:
return 1
return 0
ans = 0
for i in range(1, n+1):
ans += DFS(i, graph_s)
ans += DFS(i, graph_b)
print(ans)연습문제 3) 이분 그래프
- 문제 설명
> 그래프가 입력으로 주어지고, 이 그래프의 정점들을 인접한 정점은 다른 색으로 구분해서 그래프 정점의 집합을 둘로 분할할 수 있는지 판별 (출력 YES or NO)
=> 특정 브랜치에서 이웃 정점과 같은 색으로 이어질 수 밖에 없는 구조가 나오면 커트할 수 있으니 DFS가 좋아보인다. (인터넷에선 속도 측면에선 그닥 차이가 없는거같다.)
- 코드 설명
> dfs visit을 0, 1, -1로 구분해서 방문을 안했으면 0, 방문했으면 1, -1로 색깔 구분을 하기에 좋다.
import sys
sys.setrecursionlimit(10 ** 6)
input = sys.stdin.readline
def dfs(now, group):
vis[now] = group
for i in arr[now]:
# 아직 안가본 곳이면 방문
if vis[i] == 0:
if not dfs(i, -group):
return False
# 방문한 곳인데 색깔이 다르면 취소
elif vis[i] == vis[now]:
return False
return True
for _ in range(int(input())):
v, e = map(int, input().split())
arr = [[] for _ in range(v + 1)]
vis = [0] * (v + 1)
for _ in range(e):
x, y = map(int, input().split())
arr[x].append(y)
arr[y].append(x)
ans = True
for i in range(1, v + 1):
if vis[i] == 0:
ans = dfs(i, 1)
if not ans:
break
print("YES" if ans else "NO")
연습문제 4) 최소비용 구하기
- 문제 설명
> N개의 도시, 그 도시를 연결하는 M개의 버스. 버스를 이용하는 비용. 이를 최소화하는 문제.
=> 단방향 그래프에 간선마다의 가중치가 따로 있음.
> 도시 번호가 1부터 N까지라 리스트의 인덱스로 visit을 조회할 수 있을것임.
> 출발 도시에서 도착 도시까지 가는 최소 비용 출력
=> 다익스트라 최단 거리 알고리즘 활용.
- 코드 설명
> bfs의 알고리즘 기반으로 만들어진게 다익스트라 알고리즘인 것 같다.
> 우선 순위 queue를 사용한 방식이고, 전반적인건 BFS 구조가 동일하다.
> visit 방문 개념으로 distance에 INF or 값으로 방문 체크겸 값도 최소화하는걸로 계속 탐색이 가능하다.
import sys
import heapq
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
n = int(input())
m = int(input())
graph = [[] for i in range(n+1)]
distance = [INF] * (n+1)
for _ in range(m):
a, b, c = map(int, sys.stdin.readline().split())
graph[a].append((b,c)) # cost까지 함께 graph에 저장
s, e = map(int, sys.stdin.readline().split())
def dijkstra(start):
q = []
heapq.heappush(q, (0, start)) # 탐색 우선순위를 최소값으로 하기 위해 heap 사용
distance[start] = 0 # visit 체크하는 개념으로 값을 기입한다.
while q:
dist, now = heapq.heappop(q)
if distance[now] < dist: # visit 방문 이력 체크하는 개념
continue
for i in graph[now]: #
cost = dist + i[1]
if cost < distance[i[0]]: # 바로 가는 비용보다 둘러가는 비용이 더 싸다면 갱신
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0])) # 그 비용은 다시 heap에 넣는다.
dijkstra(s)
print(distance[e])▶ 동일 문제
18352번: 특정 거리의 도시 찾기
첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다. (2 ≤ N ≤ 300,000, 1 ≤ M ≤ 1,000,000, 1 ≤ K ≤ 300,000, 1 ≤ X ≤ N) 둘째 줄부터 M개의 줄에 걸쳐서 두 개
www.acmicpc.net
1916번: 최소비용 구하기
첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그
www.acmicpc.net
연습문제 5) 미로 만들기
- 문제 설명
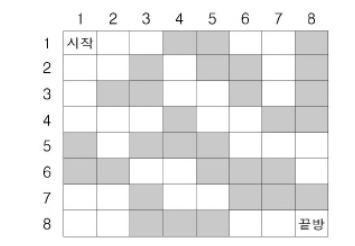
> n * n 바둑판. 시작 (1,1) -> 끝 (n,n)으로 가는데 검은 벽으로는 갈 수가 없다. 하지만 흰 방으로만 갈 수 없을 땐, 검은방을 흰방으로 바꿀 수 있다. 구하는 답은 끝으로 가는데 색을 변경해야하는 최소의 수를 구하라.
> 컴퓨터는 value하나씩 판단하기 때문에 일일이 다녀보지 않으면 알 수 없다. 하지만 어떻게 효율적으로 탐색할 수 있을까를 생각해야한다.
> 너비 우선으로 탐색을 하면서 중간에 핸디캡을 주는 방식으로 우선 순위 큐를 이용하면 된다.
- 코드 설명
> 미로도 위 문제와 동일하게 다익스트라로 풀면 될거같다. 길에 조건을 넣어서 검은 방이면 +1을 해주는 식을 핸드캡을 줬다.
> cost라는 리스트가 visit 방문 이력과 원하는 최소 변경 수를 저장해나갈 수 있다.
import sys
import heapq
INF = int(1e9)
n = int(sys.stdin.readline().strip())
miro = [list(map(int, list(sys.stdin.readline().rstrip()))) for i in range(n)]
t_cost = [[INF] * (n) for _ in range(n)]
visited = [[False] * n for _ in range(n)]
def dijkstra(r, c):
q = []
heapq.heappush(q, (0, r, c))
t_cost[r][c] = 0
while q:
cost, row, col = heapq.heappop(q)
visited[row][col] = True
if t_cost[row][col] < cost:
continue
if row == n-1 and col == n-1:
return t_cost[n-1][n-1]
for dx, dy in ((-1,0), (0,1), (1,0), (0, -1)):
nx = row + dx
ny = col + dy
if 0 <= nx <= n-1 and 0 <= ny <= n-1:
if miro[nx][ny] != 0: #nx와 ny가 방문한 적이 없으며, miro상에서도 흰방일 경우, cost는 1만 더한다.
tmp = cost
if tmp < t_cost[nx][ny]:
t_cost[nx][ny] = tmp
heapq.heappush(q, (tmp, nx, ny))
elif miro[nx][ny] == 0: #nx와 ny가 방문한 적이 없으며, miro상에서도 검은 방일 경우, cost는 2를 더한다. (핸디캡)
tmp = cost + 1
if tmp < t_cost[nx][ny]:
t_cost[nx][ny] = tmp
heapq.heappush(q, (tmp, nx, ny))
print(dijkstra(0,0))연습문제 6) 탈출 (백준 3055번)
- 문제설명
> 행렬 n * m 지도. 고슴도치('S')는 홍수('*')를 피해 비버의 굴('D')로 가야한다. 조건은 물('*')은 비버의 굴('D')이나 돌('X')로 못 가고 고슴도치도 돌('X')이 있는곳을 못 간다. 고슴도치가 비버의 굴로 이동하는 가장 빠른 시간은? 안전하게 갈 수없다면 "KAKTUS" 출력

- 코드 설명
> 이동하는 객체는 물과 고슴도치 두개다. 물 > 고슴도치 우선 순위로 popleft할 수 있게 하면 된다.
> 제약 조건은 물에게는 비버굴과 돌이고, 고슴도치에겐 돌이 있다. (방문시 조건 추가)
> 동시에 점진적으로 진행하면서 제약사항을 반영하므로 BFS를 활용하는게 좋을듯 하다.
import sys
from collections import deque
input = sys.stdin.readline
def bfs():
while q:
x, y, w = q.popleft()
for dx, dy in ((-1,0), (0,1), (1,0), (0,-1)):
nx, ny = x + dx, y + dy
if nx < 0 or ny < 0 or nx >= n or ny >= m: continue
if a[nx][ny] == 'D':
if w: continue
return dist[x][y] # 당연히 D에는 dist 기록이 없기 떄문에 x, y의 값으로 출력
if dist[nx][ny] or a[nx][ny] == 'X': continue #방문기록이 있거나 x라면 진행x
dist[nx][ny] = dist[x][y] + 1
q.append((nx,ny,w))
return "KAKTUS"
n, m = map(int, input().split())
a = [list(input().strip()) for _ in range(n)]
q = deque()
dist = [[0]*m for _ in range(n)]
for i in range(n):
for j in range(m):
if a[i][j] == 'S':
x, y = i, j
dist[i][j] = 1 # 마지막 한 칸을 안간 채로 print하기 때문에
elif a[i][j] == '*':
q.append((i, j, 1))
dist[i][j] = 1
q.append((x, y, 0))
print(bfs())'알고리즘' 카테고리의 다른 글
| [Python] 백준 14501번 퇴사 (0) | 2021.11.27 |
|---|---|
| [Python] 백준 1149번 RGB거리 (0) | 2021.11.26 |
| [Python] 백준 21606번 아침 산책 (0) | 2021.11.21 |
| [Python] 백준 2573번 빙산 (0) | 2021.11.21 |
| [Algorithm] 다익스트라 알고리즘 (0) | 2021.11.21 |


