알고리즘
선형탐색과 이진탐색
하루설렘
2021. 11. 11. 21:45
백준 1920 수찾기를 선형탐색과 이진탐색으로 풀면서 들었던 의문이다.
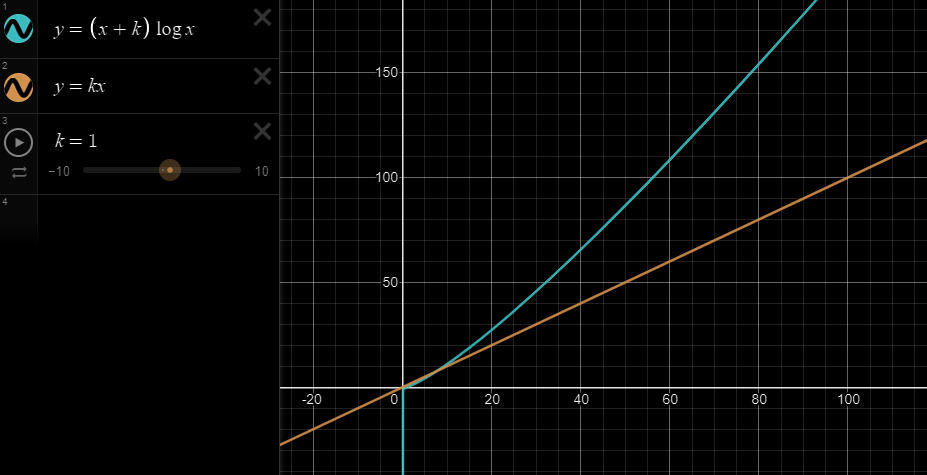
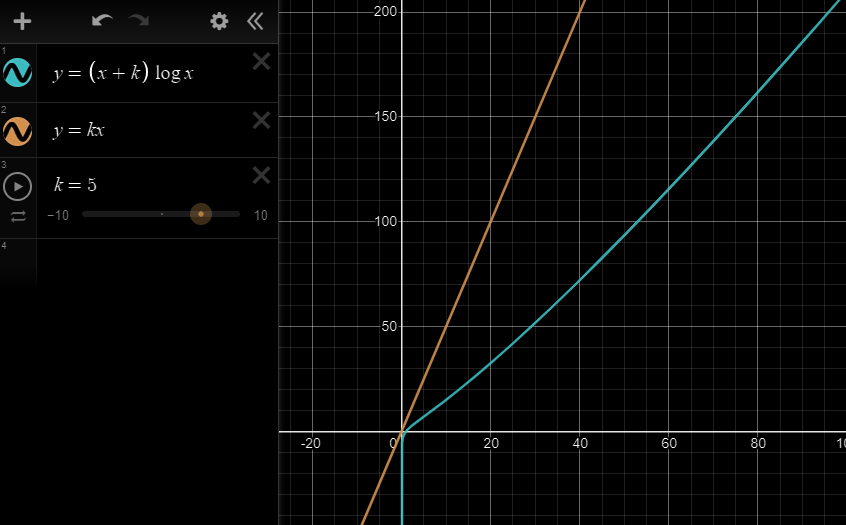
Sort한 후, 이진탐색(binary search)를 할 경우 선형탐색(Linear search) 대비 느려질거라 생각했지만? 실제론 더 빠른 결과를 얻었다. 왜 그럴까?
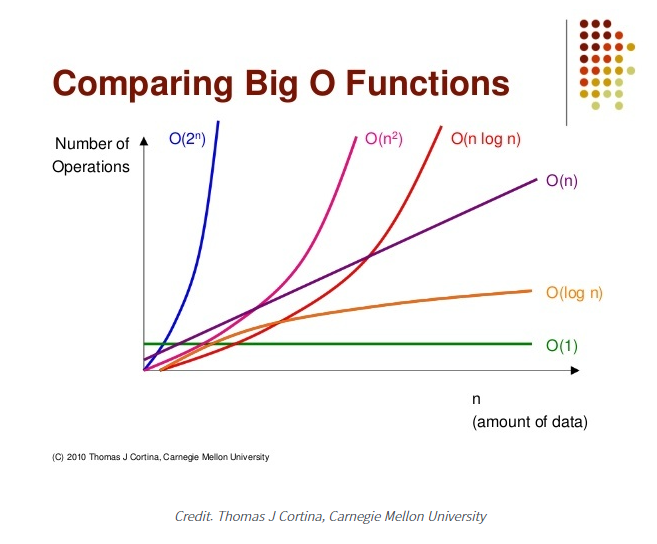
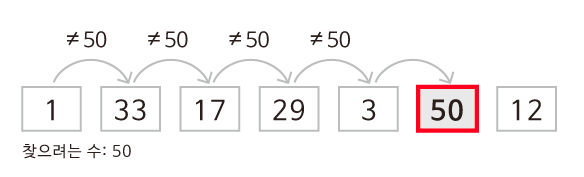
선형탐색 (Linear search)은 배열의 맨 앞 원소부터 맨 끝 원소까지 탐색하기에 시간 복잡도는 O(N)이다.
이 때, 최상/평균/최악의 case가 있는데, 알고리즘 성능을 얘기하기 위해선 최악의 case로 계산한다.
참고 블로그: https://hahasof.tistory.com/5
이진탐색은 정렬되어있는 배열 중간값과 비교해서 탐색해나가서 시간 복잡도는 O(logN)이 된다.
처음에 입력된 갯수를 N 이라하면,
첫 시행 후에는 반이 버려져서

,
두 번째 시행 후에는 또 그 반이 버려져서
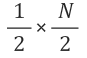
,
새 번째 시행 후에는 또 그 반이 버려져서
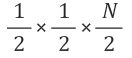
,
규칙이 보이시나요? 그렇습니다. 매 시행마다 탐색할 자료의 개수가 점점 반씩 줄어드는 걸 알 수 있죠.
그럼 K 번의 시행 후에는?
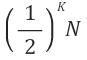
개가 남게 되겠죠.
이렇게 계속해서 탐색을 반복하다보면 탐색이 끝나는 시점에는 (최악의 경우 즉, 찾는 데이터가 없는 경우) 남은 자료가 1개가 남게 되겠죠.
따라서,

라고 표기할 수 있겠군요.
마지막으로 양 변에 2를 밑으로 하는 로그를 취해주면,

출처: https://jwoop.tistory.com/9
하지만, 정렬이 되어있지 않은 경우, sort함수를 사용하면, 최소 NlogN으로 이진탐색이 느려질거라 생각했지만?
실제론 더 빠른 결과를 얻었다. 왜 그럴까?
찾아 보니 이런 내용이 있었다.